统计3：区间估计

置信水平

一个置信水平1-α的区间估计的含义是，得到的区间以1-α覆盖被估的参数

基本方法

1. 构造枢轴量pivot，$G(x_1,\ldots,x_n,\theta)$

   要求,G的分布不依赖于参数$\theta$,否则第2步无法解出不等式

2. 找到G的边界适当选取两个常数c,d,对给定的$\alpha有P(c\leq G\leq d)\geq 1- α$

3. 求解$c\leq G(x_1,\ldots,x_n,\theta)\leq d$,得到$\theta$的两个估计值边界

预知识

卡方分布

假设$X_1, X_2, \ldots, X_k$是独立同分布（iid）的标准正态分布（即均值为0，方差为1），那么定义随机变量($Y = X_1^2 + X_2^2 + \ldots + X_k^2$)，则(Y)服从自由度为(k)的卡方分布。

数学公式表示为：
$Y \sim \chi^2(k)$

其中，X是符合卡方分布的随机变量，k是自由度。

t分布（t-distribution）

假设X是来自标准正态分布的随机变量，Y是来自卡方分布的自由度为k的随机变量（独立于X），则定义随机变量$T = \frac{X}{\sqrt {Y/k} }$，则T服从自由度为k的t分布。

数学公式表示为： $T \sim t(k)$

其中，T是符合t分布的随机变量，k是自由度。

F分布（F-distribution）

假设Y1是来自自由度为k1的卡方分布的随机变量，Y2是来自自由度为k2的卡方分布的随机变量（两者独立），则定义随机变量$F = \frac{ {Y1}/{k1} } { {Y2}/ {k2} }$，则F服从自由度为k1和k2的F分布。

数学公式表示为： $F \sim F(k1, k2)$

其中，F是符合F分布的随机变量，k1和k2是自由度。

解题方法

背就完事了

$1.N(\mu,\sigma^2),\sigma2已知,\mu未知,求\mu$

$G=\frac {\sqrt n (\bar x - \mu)} \sigma \sim N(0,1)$,$d=u_{1-\alpha/2},c=u_{\alpha/2}=-u_{1-\alpha/2}$

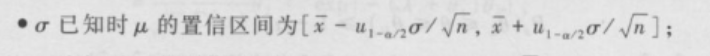
$2.N(\mu,\sigma^2),\sigma2未知,\mu未知,求\mu$

由于$\sigma$未知,所以想办法约掉$\sigma$:
$$
\frac {(n-1)s^2}{\sigma2}\sim \chi^2(n-1)
$$

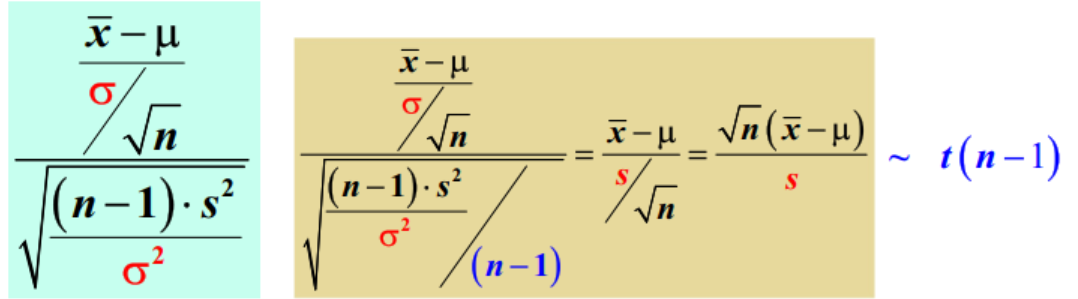
$d=t_{1-\alpha/2}(n-1),c=-t_{1-\alpha/2}(n-1)$

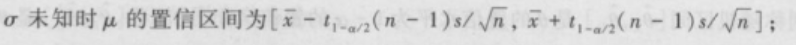
$3.N(\mu,\sigma^2),\sigma2未知,\mu未知,求\sigma^2$

$$
\frac {(n-1)s^2}{\sigma2}\sim \chi^2(n-1)
$$

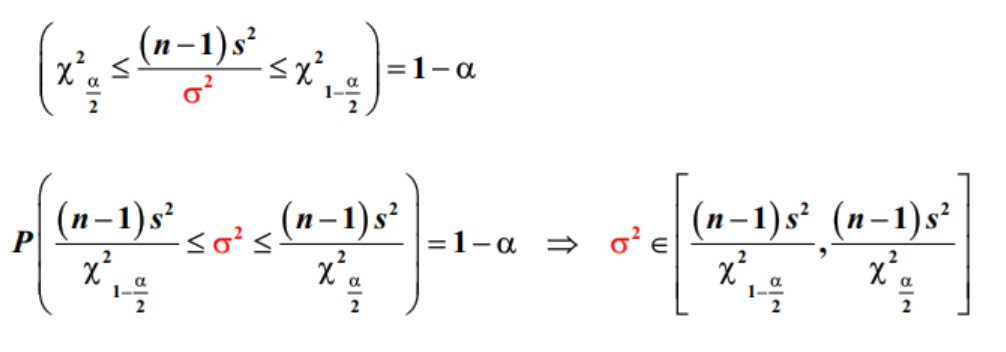
4.

大样本区间估计

样本容量足够大时,用样本统计量替换总体统计量