统计4:假设检验
$H_0 : \theta\in\Theta_0~~~ vs~~~ H_1 : \theta\in\Theta_1$
假设检验是一种统计方法,用于评估关于总体参数的假设是否与观察到的样本数据一致。
总的原理是假如试验结果与假设日发生矛盾就拒绝原假设 也否则就接受原假设.
定义
-
(统计)假设检验问题
这是在给定总体与样本下 ,要求对命题做出判断。
-
(统计)假设
统计学中两个非空不相交参数集合$\Theta_0,\Theta_1$,命题成立对应$\theta\in\Theta_0$,否则$\theta\in\Theta_1$
-
参数假设检验问题
假设可用一个参数的集合表示的假设检验问题
例子:
-
均值是否大于4是参数假设检验问题
-
是否为正态分布不是,不能用一个参数的集合检验
-
-
检验(法则)
通过样本对假设做出判断
-
原(零)假设$\Theta_0$与对立(备择)假设$\Theta_1$
-
如果$\Theta_0$只含一个点则称为是简单的,否则是复杂的
-
$H_0 : \theta\in\Theta_0~~~ vs~~~ H_1 : \theta\in\Theta_1$
-
接受域:样本空间接受H_0的区域
确定了接受域和拒绝域,只需要看样本属于哪个样本空间就完成检验了
-
-
错误
-
第一类错误
本应接受,结果拒绝,犯错概率称为α(θ)
-
第二类错误
本应拒绝,结果接受,犯错概率称为β(θ)
由于不可能同时降低这两个错误,所以我们仅控制第一类错误.宁肯放过一千,也不错杀一个.
-
-
势函数g(θ)
样本落在拒绝域内的概率
$$
\theta\in\Theta_0,g(\theta)=\alpha(\theta),\
\theta\in\Theta_1,g(\theta)=1-\beta(\theta)
$$ -
显著性水平$\alpha$
对任意的$\Theta_0$中$\theta$,都有势函数$\leq$α
控制第一类犯错的概率在α内
-
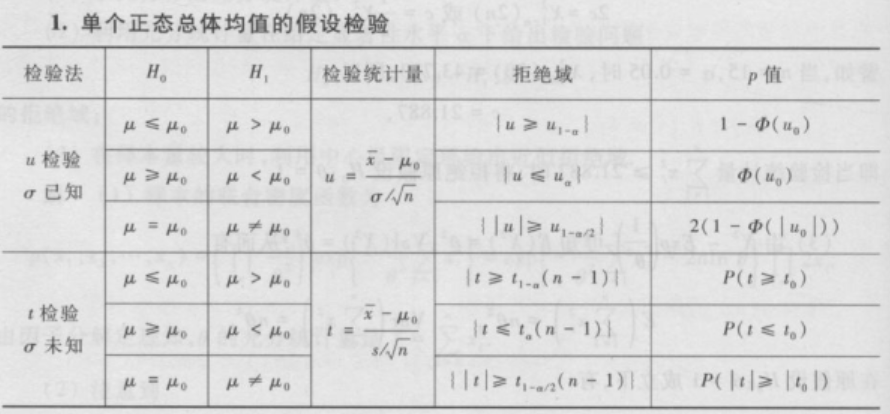
U检验
方差已知,对正态总体均值进行检验
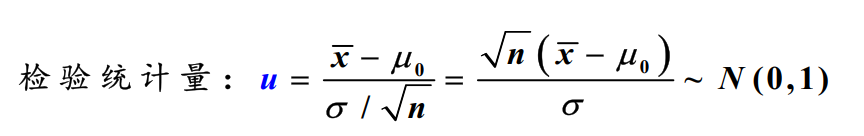
-
t检验
方差未知,对正态总体均值进行检验
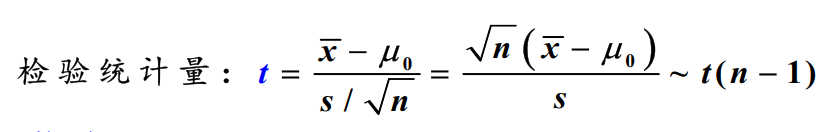
-
p值
-
利用样本观测值能够做出拒绝原假设的最小显著性水平
原假设成立条件下,检验统计量出现在比观测值更异常的范围的概率的最大值
基本步骤
-
建立假设
- $H_0 : \theta\in\Theta_0~~~ vs~~~ H_1 : \theta\in\Theta_1$
-
选择检验统计量,给出拒绝域的形式
-
选择显著性水平,给出拒绝域的具体范围
例题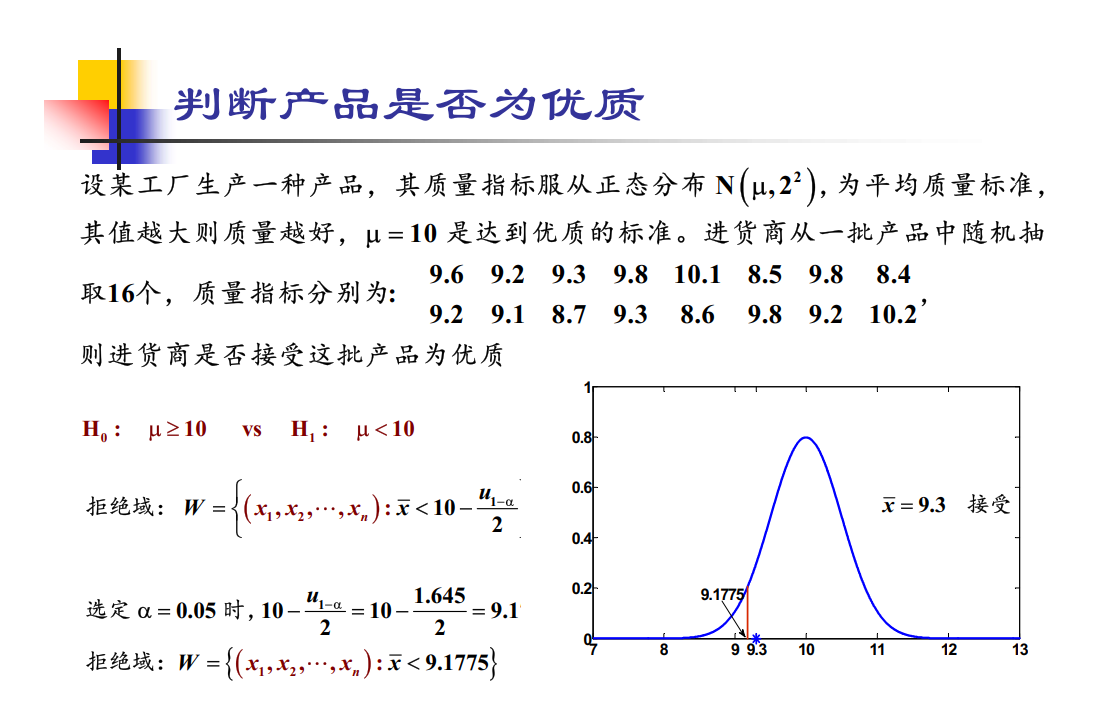
-
建立假设(H_0,优质,μ$\geq$10)
注意这里优劣并不一定对应原假设/对立假设。
按照过去长时间的记录,商店的检验人员相信该厂的产品质量很好,可能选择μ>10为原假设
如果认为不好也可能选择μ<10为原假设
-
选择检验统计量
$\bar x\sim N(\mu,\frac {2^2} {16} )$,拒绝域形式为{(样本),$\bar x$<c}
-
确定显著性水平
$$
P(\bar x<c|\mu = 10)=\alpha\
P\left(\frac {\bar x-10} {1/2}<\frac {c-10} {1/2}\right)=\alpha,\frac {\bar x-10} {1/2}\sim N(0,1)
$$
如果这里α取0.05,那么可以求得c=10+$2u_{0.05}$
-
$\bar x>c$时,接受原假设,否则拒绝